Показательная функция. Урок «Показательная функция, ее свойства и график
ПОКАЗАТЕЛЬНАЯ И ЛОГАРИФМИЧЕСКАЯ ФУНКЦИИ VIII
§ 179 Основные свойства показательной функции
В этом параграфе мы изучим основные свойства показательной функции
у = а x (1)
Напомним, что под а в формуле (1) мы подразумеваем любое фиксированное положительное число, отличное от 1.
Свойство 1. Областью определения показательной функции является совокупность всех действительных чисел.
В самом деле, при положительном а выражение а x определено для любого действительного числа х .
Свойство 2 . Показательная функция принимает только положительные значения.
Действительно, если х > 0, то, как было доказано в § 176,
а x > 0.
Если же х <. 0, то
а x =
где - х уже больше нуля. Поэтому а - x > 0. Но тогда и
а x = > 0.
Наконец, при х = 0
а x = 1.
2-е свойство показательной функции имеет простое графическое истолкование. Оно заключается в том, что график этой функции (см. рис. 246 и 247) располагается целиком выше оси абсцисс.

Свойство 3 . Если а >1, то при х > 0 а x > 1, а при х < 0 а x < 1. Если же а < 1, то, наоборот, при х > 0 а x < 1, а при х < 0 а x > 1.
Это свойство показательной функции также допускает простую геометрическую интерпретацию. При а > 1 (рис. 246) кривые у = а x располагаются выше прямой у = 1 при х > 0 и ниже прямой у = 1 при х < 0.
Если же а < 1 (рис. 247), то, наоборот, кривые у = а x располагаются ниже прямой у = 1 при х > 0 и выше этой прямой при х < 0.
Приведем строгое доказательство 3-го свойства. Пусть а > 1 и х - произвольное положительное число. Покажем, что
а x > 1.
Если число х рационально (х = m / n ) , то а x = а m / n = n √a m .
Поскольку а > 1, то и а m > 1, Но корень из числа, большего единицы, очевидно, также больше 1.
Если х иррационально, то существуют положительные рациональные числа х" и х" , которые служат десятичными приближениями числа x :
х" < х < х" .
Но тогда по определению степени с иррациональным показателем
а x" < а x < а x"" .
Как показано выше, число а x" больше единицы. Поэтому и число а x , большее, чем а x" , также должно быть больше 1,
Итак, мы показали, что при a >1 и произвольном положительном х
а x > 1.
Если бы число х было отрицательным, то мы имели бы
а x =
где число -х было бы уже положительным. Поэтому а - x > 1. Следовательно,
а x = < 1.
Таким образом, при а > 1 и произвольном отрицательном x
а x < 1.
Случай, когда 0 < а < 1, легко сводится к уже рассмотренному случаю. Учащимся предлагается убедиться в этом самостоятельно.
Свойство 4. Если х = 0, то независимо от а а x =1.
Это вытекает из определения нулевой степени; нулевая степень любого числа, отличного от нуля, равна 1. Графически это свойство выражается в том, что при любом а кривая у = а x (см. рис. 246 и 247) пересекает ось у в точке с ординатой 1.
Свойство 5. При а >1 показательная функция у = а x является монотонно возрастающей, а при а < 1 - монотонно убывающей.
Это свойство также допускает простую геометрическую интерпретацию.
При а > 1 (рис. 246) кривая у = а x с ростом х поднимается все выше и выше, а при а < 1 (рис. 247) - опускается все ниже и ниже.
Приведем строгое доказательство 5-гo свойства.
Пусть а > 1 и х 2 > х 1 . Покажем, что
а x 2 > а x 1
Поскольку х 2 > х 1 ., то х 2 = х 1 + d , где d -некоторое положительное число. Поэтому
а x 2 - а x 1 = а x 1 + d - а x 1 = а x 1 (а d - 1)
По 2-му свойству показательной функции а x 1 > 0. Так как d > 0, то по 3-му свойству показательной функции а d > 1. Оба множителя в произведении а x 1 (а d - 1) положительны, поэтому и само это произведение положительно. Значит, а x 2 - а x 1 > 0, или а x 2 > а x 1 , что и требовалось доказать.
Итак, при a > 1 функция у = а x является монотонно возрастающей. Аналогично доказывается, что при а < 1 функция у = а x является монотонно убывающей.
Следствие. Если две степени одного и того же положительного числа, отличного от 1, равны, то равны и их показатели.
Другими словами, если
а b = а c (а > 0 и а =/= 1),
b = с .
Действительно, если бы числа b и с были не равны, то в силу монотонности функции у = а x большему из них соответствовало бы при а >1 большее, а при а < 1 меньшее значение этой функции. Таким образом, было бы или а b > а c , или а b < а c . И то и другое противоречит условию а b = а c . Остается признать, что b = с .
Свойство 6. Если а > 1, то при неограниченном возрастании аргумента х (х -> ∞ ) значения функции у = а x также неограниченно растут (у -> ∞ ). При неограниченном убывании аргумента х (х -> -∞ ) значения этой функции стремятся к нулю, оставаясь при этом положительными (у ->0; у > 0).
Принимая во внимание доказанную выше монотонность функции у = а x , можно сказать, что в рассматриваемом случае функция у = а x монотонно возрастает от 0 до ∞ .
Если 0 < а < 1, то при неограниченном возрастании аргумента х (х -> ∞) значения функции у = а x стремятся к нулю, оставаясь при этом положительными (у ->0; у > 0). При неограниченном убывании аргумента х (х -> -∞ ) значения этой функции неограниченно растут (у -> ∞ ).
В силу монотонности функции у = а x можно сказать, что в этом случае функция у = а x монотонно убывает от ∞ до 0.
6-е свойство показательной функции наглядно отражено на рисунках 246 и 247. Строго доказывать его мы не будем.
Нам осталось лишь установить область изменения показательной функции у = а x (а > 0, а =/= 1).
Выше мы доказали, что функция у = а x принимает только положительные значения и либо монотонно возрастает от 0 до ∞ (при а > 1), либо монотонно убывает от ∞ до 0 (при 0 < а <. 1). Однако остался невыясненным следующий вопрос: не претерпевает ли функция у = а x при своем изменении каких-нибудь скачков? Любые ли положительные значения она принимает? Вопрос этот решается положительно. Ecли а > 0 и а =/= 1, то, каково бы ни было положительное число у 0 обязательно найдется х 0 , такое, что
а x 0 = у 0 .
(В силу монотонности функции у = а x указанное значение х 0 будет, конечно, единственным.)
Доказательство этого факта выходит за пределы нашей программы. Геометрическая интерпретация его состоит в том, что при любом положительном значении у 0 график функции у = а x обязательно пересечется с прямой у = у 0 и притом лишь в одной точке (рис. 248).

Отсюда можно сделать следующий вывод, который мы формулируем в виде свойства 7.
Свойство 7. Областью изменения показательной функции у = а x (а > 0, а =/= 1) служит множество всех положительных чисел.
Упражнения
1368. Найти области определения следующих функций:
1369. Какие из данных чисел больше 1 и какие меньше 1:

1370. На основании какого свойства показательной функции можно утверждать, что
а) (5 / 7) 2,6 > (5 / 7) 2,5 ; б) (4 / 3) 1,3 > (4 / 3) 1,2
1371. Какое число больше:
а) π - √3 или (1 / π ) - √3 ; в) (2 / 3) 1 + √6 или (2 / 3) √2 + √5 ;
б) ( π / 4) 1 + √3 или ( π / 4) 2 ; г) (√3 ) √2 - √5 или (√3 ) √3 - 2 ?
1372. Равносильны ли неравенства:
1373. Что можно сказать о числах х и у , если а x = а y , где а - заданное положительное число?
1374. 1) Можно ли среди всех значений функции у = 2 x выделить:
2) Можно ли среди всех значений функции у = 2 | x| выделить:
а) наибольшее значение; б) наименьшее значение?
1.Показательная функция – это функция вида у(х) =а х, зависящая от показателя степени х, при постоянном значении основания степени a , где а > 0, a ≠ 0, xϵR (R – множество действительных чисел).
Рассмотрим график функции, если основание не будет удовлетворять условию: а>0
a) a < 0
Если a < 0 – возможно возведение в целую степень или в рациональную степень с нечетным показателем.
а = -2

Если а = 0 – функция у = определена и имеет постоянное значение 0

в) а =1
Если а = 1 – функция у = определена и имеет постоянное значение 1
Область определения функции (ООФ) Область допустимых значений функции (ОДЗ) 3. Нули функции (у = 0) 4. Точки пересечения с осью ординат oy (x = 0) 5. Возрастания, убывания функции Если , то функция f(x) возрастает 6. Чётность, нечётность функции Функция у = не симметрична относительно оси 0у и относительно началу координат, следовательно не является ни чётной, ни нечётной. (Функция общего вида) 7. Функция у = экстремумов не имеет 8. Свойства степени с действительным показателем: Пусть а > 0; a≠1 Тогда для xϵR; yϵR: Свойства монотонности степени: если , то Если a> 0, , то . 9. Относительное расположение фунцкции Чем больше основание а, тем ближе к осям ох и оу a > 1, a = 20 Пример 1. Введем сначала определение показательной функции. Показательная функция $f\left(x\right)=a^x$, где $a >1$. Введем свойства показательной функции, при $a >1$.
\ \[корней\ нет.\] \ Пересечение с осями координат. Функция не пересекает ось $Ox$, но пересекает ось $Oy$ в точке $(0,1)$. $f""\left(x\right)={\left(a^xlna\right)}"=a^x{ln}^2a$
\ \[корней\ нет.\] \ График (рис. 1). Рисунок 1. График функции $f\left(x\right)=a^x,\ при\ a >1$.
Введем свойства показательной функции, при $0 Область определения -- все действительные числа. $f\left(-x\right)=a^{-x}=\frac{1}{a^x}$ -- функция ни четна, ни нечетна. $f(x)$ - непрерывна на всей области определения. Область значения -- интервал $(0,+\infty)$. $f"(x)=\left(a^x\right)"=a^xlna$
\ \[корней\ нет.\] \ \[корней\ нет.\] \ Функция выпукла на всей области определения. Поведение на концах области определения:
\[{\mathop{lim}_{x\to -\infty } a^x\ }=+\infty \] \[{\mathop{lim}_{x\to +\infty } a^x\ }=0\] График (рис. 2). Исследовать и построить график функции $y=2^x+3$. Решение.
Проведем исследование по примеру схемы выше: Область определения -- все действительные числа. $f\left(-x\right)=2^{-x}+3$ -- функция ни четна, ни нечетна. $f(x)$ - непрерывна на всей области определения. Область значения -- интервал $(3,+\infty)$. $f"\left(x\right)={\left(2^x+3\right)}"=2^xln2>0$ Функция возрастает на всей области определения. $f(x)\ge 0$ на всей области определения. Пересечение с осями координат. Функция не пересекает ось $Ox$, но пересекает ось $Oy$ в точке ($0,4)$ $f""\left(x\right)={\left(2^xln2\right)}"=2^x{ln}^22>0$ Функция выпукла на всей области определения. Поведение на концах области определения:
\[{\mathop{lim}_{x\to -\infty } a^x\ }=0\] \[{\mathop{lim}_{x\to +\infty } a^x\ }=+\infty \] График (рис. 3). Рисунок 3. График функции $f\left(x\right)=2^x+3$
Найдем значение выражения при различных рациональных значениях переменной х=2; 0; -3; - Заметим, какое бы число вместо переменной икс мы не подставили, всегда можно найти значение данного выражения. Значит, мы рассматриваем показательную функцию (игрек равен три в степени икс), определенную на множестве рациональных чисел: . Построим график данной функции, составив таблицу ее значений. Проведем плавную линию, проходящую через данные точки (рис 1) Используя график данной функции, рассмотрим ее свойства: 3.Возрастает на всей области определения. 8. Функция выпукла вниз. Если в одной системе координат построить графики функций; у=(игрек равен два в степени икс, игрек равен пять в степени икс, игрек равен семь в степени икс), то можно заметить, что они обладают теми же свойствами, что и у=(игрек равен трем в степени икс) (рис.2), то есть такими свойствами будут обладать все функции вида у=(игрек равен а в степени икс, при а большем единицы) Построим график функции: 1. Составив таблицу ее значений. Отметим полученные точки на координатной плоскости. Проведем плавную линию, проходящую через данные точки (рис 3). Используя график данной функции, укажем ее свойства: 1. Область определения - множество всех действительных чисел. 2.Не является ни четной, ни нечетной. 3.Убывает на всей области определения. 4.Не имеет ни наибольшего, ни наименьшего значений. 5.Ограничена снизу, но не ограничена сверху. 6.Непрерывна на всей области определения. 7. область значения от нуля до плюс бесконечности. 8. Функция выпукла вниз. Аналогично, если в одной системе координат построить графики функций; у=(игрек равен одна вторая в степени икс, игрек равен одна пятая в степени икс, игрек равен одна седьмая в степени икс), то можно заметить, что они обладают теми же свойствами, что и у=(игрек равен одна третья в степени икс)(рис.4), то есть такими свойствами будут обладать все функции вида у=(игрек равен единица, деленная на а в степени икс, при а большем нуля, но меньшем единицы) Построим в одной системе координат графики функций значит, будут симметричны и графики функций у=у= (игрек равен а в степени икс и игрек равен единице, деленной на а в степени икс) при одном и том же значении а. Обобщим сказанное, дав определение показательной функции и указав ее основные свойства: Определение:
Функция вида у=, где (игрек равен а в степени икс, где а положительно и отлично от единицы), называют показательной функцией. Необходимо запомнить различия между показательной функцией у= и степенной функцией у=, а=2,3,4,…. как на слух, так и зрительно. У показательной функции х
является степенью, а у степенной функции х
является основанием. Пример1: Решите уравнение (три в степени икс равно девяти) (игрек равняется три в степени икс и игрек равняется девяти) рис.7 Заметим, что они имеют одну общую точку М (2;9) (эм с координатами два; девять), значит, абсцисса точки будет являться корнем данного уравнения. То есть, уравнение имеет единственный корень х= 2. Пример 2: Решите уравнение В одной системе координат построим два графика функции у= (игрек равен пяти в степени икс и игрек равен одна двадцать пятая) рис.8. Графики пересекаются в одной точке Т (-2;(тэ с координатами минус два; одна двадцать пятая). Значит, корнем уравнения является х=-2(число минус два). Пример 3: Решите неравенство В одной системе координат построим два графика функции у= (игрек равен три в степени икс и игрек равен двадцати семи). Рис.9 График функции расположен выше графика функции у=при х Следовательно, решением неравенства является интервал (от минус бесконечности до трех) Пример 4: Решите неравенство В одной системе координат построим два графика функции у= (игрек равен одна четвертая в степени икс и игрек равен шестнадцати). (рис.10). Графики пересекаются в одной точке К (-2;16). Значит, решением неравенства является промежуток (-2;(от минус двух до плюс бесконечности), т.к. график функции у=расположен ниже графика функции при х Наши рассуждения позволяют убедиться в справедливости следующих теорем: Терема 1: Если справедливо тогда и только тогда, когда m=n. Теорема 2: Если справедливо тогда и только тогда, когда, неравенство справедливо тогда и только тогда, когда (рис. *) Теорема 4: Если справедливо тогда и только тогда, когда (рис.**), неравенство справедливо тогда и только тогда, когда.Теорема 3: Если справедливо тогда и только тогда, когда m=n. Пример 5: Построить график функции у= Видоизменим функцию, применив свойство степени у= Построим дополнительную систему координат и в новой системе координат построим график функции у= (игрек равен два в степени икс) рис.11. Пример 6: Решите уравнение В одной системе координат построим два графика функции у= (игрек равен семи в степени икс и игрек равен восемь минус икс) рис.12. Графики пересекаются в одной точке Е (1;(е с координатами один; семь). Значит, корнем уравнения является х=1(икс равный единице). Пример 7: Решите неравенство В одной системе координат построим два графика функции у= (игрек равен одна четвертая в степени икс и игрек равен икс плюс пять). График функции у=расположен ниже графика функции у=х+5 при, решением неравенства является интервал х(от минус единицы до плюс бесконечности). Концентрация внимания:
Определение. Функция
вида называется показательной
функцией
. Замечание. Исключение из числа значений
основания a
чисел 0; 1 и отрицательных значений a
объясняется следующими обстоятельствами: Само аналитическое выражение a x
в
указанных случаях сохраняет смысл и может
встречаться в решении задач. Например, для
выражения x y
точка x = 1; y
= 1
входит
в область допустимых значений. Построить графики функций: и . Свойства показательной функции Когда заполняется таблица, то параллельно с
заполнением решаются задания. Задание № 1. (Для нахождения области
определения функции). Какие значения аргумента являются допустимыми для функций: Задание № 2. (Для нахождения области
значений функции). На рисунке изображен график функции. Укажите
область определения и область значений функции: Задание № 3. (Для указания промежутков
сравнения с единицей). Каждую из следующих степеней сравните с
единицей: Задание № 4. (Для исследования функции на
монотонность). Сравнить по величине действительные числа m
и n
если: Задание № 5. (Для исследования функции на
монотонность). Сделайте заключение относительно основания a
,
если: y(x) = 10 x ; f(x) = 6 x ; z(x) - 4 x
Как располагаются графики показательных
функций относительно друг друга при x > 0, x = 0, x <
0? В одной координатной плоскости построены
графики функций: y(x) = (0,1) x ; f(x) = (0,5) x ; z(x) = (0,8) x .
Как располагаются графики показательных
функций относительно друг друга при x > 0, x = 0, x <
0? Число e
играет особую роль в математическом анализе. Показательная
функция
с основанием e
, называется
экспонентой
и обозначается y = e x
. Первые знаки числа
e
запомнить
несложно: два, запятая, семь, год рождения
Льва Толстого - два раза, сорок пять, девяносто,
сорок пять.
Домашнее задание: Колмогоров п. 35; № 445-447; 451; 453. Повторить алгоритм построения графиков
функций, содержащих переменную под знаком
модуля. 
2. Рассмотрим подробнее показательную функцию:
0


Если , то функция f(x) убывает
Функция y= , при 0
Это следует из свойств монотонности степени с действительным показателем.
b> 0; b≠1
Например:


Показательная функция непрерывна в любой точке ϵ R.


Если а0, то показательная функция принимает вид близкий к y = 0.
Если а1, то дальше от осей ох и оу и график принимает вид близкий к функции у = 1.
Построить график у =
Показательная функция $f\left(x\right)=a^x$, где $0
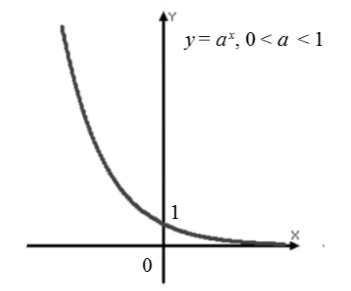
Пример задачи на построение показательной функции




График показательной функции
y =
a x
, a > 1
y =
a x
, 0< a < 1
Свойства показательной функции
y =
a x
, a > 1
y =
a x
, 0< a <
1
2. Область значений функции
3.Промежутки сравнения с
единицей
при x
> 0, a x
>
1
при x
> 0, 0< a x
< 1
при x
< 0, 0< a x
< 1
при x
< 0, a x
>
1
4. Чётность, нечётность.
Функция не является ни
чётной, ни нечётной (функция общего вида).
5.Монотонность.
монотонно возрастает на R
монотонно убывает на R
6. Экстремумы.
Показательная функция
экстремумов не имеет.
7.Асимптота
Ось O x
является
горизонтальной асимптотой.
8. При любых действительных
значениях x
и y
;
Число
одна из важнейших постоянных в математике. По
определению, оно равно пределу
последовательности
при
неограниченном
возрастании n
.
Обозначение e
ввёл Леонард Эйлер
в 1736 г. Он вычислил первые 23 знака этого числа в
десятичной записи, а само число назвали в честь
Непера «неперовым числом».








